A Gentle Introduction to Static Verification and Bug Finding with CiaoPP
Author(s): Daniela Ferreiro, Jose F. Morales (minor), Manuel Hermenegildo (minor).This is a tutorial to illustrate step-by-step the development of a program for a given specification, using the Ciao language of assertions, which allows the user to describe predicates and properties. Our aim is to show how to use CiaoPP to prove statically whether these assertions hold and/or detect bugs. The tutorial also provides an introduction to the dynamic checking aspects of CiaoPP. Although the solution of the different exercises is provided in this tutorial, try to think first about the answer on your own, and experiment!
Consider the following specification (taken from the Prolog programming contest at ICLP'95, Portland, USA):
In the following section we will show a complete, fully working Initial implementation. If you wish, you can skip directly to this solution and run some queries before we start specifying properties Using assertions.
- Some code boxes need your interaction. You will identify them by a question mark (?) in the right top corner.
- Your goal is to turn all question marks in such boxes into green checked marks (✔):
- Boxes with a thinking face (🤔) are exercises that you must complete in order to progress. Once an exercise is completed, press the question mark.
- Boxes without the thinking face just need pressing the question mark. They are editable so that you can play with them.
- Code errors or failed exercises turn the question mark into a red erroneous mark (✘). You can try again as many times as you want.
- When available, pressing the northeast pointing arrow (↗) will load the code into a separate playground window.
- Additionally, boxes with right-pointing triangles (▶) allow interacting with the code loaded so far, by issuing queries. In order to use these query boxes, make sure the previous code boxes are checked (✔), to ensure that the corresponding code has been loaded.
Defining modules and exports
We will start with the module declaration::- module(powers,[powers/3],[assertions])This module declaration states that the name of the module is powers, that it exports a predicate powers/3, and that it uses the assertions package. Note that the powers module will define other predicates, such as remove_power/3 (again, the program can be found below). These other predicates are internal to the module, i.e., they cannot be seen or used in other modules. One of the reasons why we export only the powers/3 predicate is that this allows CiaoPP to assume during the analysis of this program that external calls are made only to this predicate. This fact will allow CiaoPP to produce more accurate information about the program, since analysis then does not have to consider all the possible ways in which other predicates inside the module may be called, and only those that can actually occur in the module.Writing powers/3
Once we have defined the module we start writing the powers/3 predicate. We can sketch the main idea of our approach with a motivating example. Consider the following query:
?- powers([2,3,5],7,Powers).We start by constructing the list of pairs [(2,2),(3,3),(5,5)], which is sorted and which has no two pairs with the same first component. The implementation of this predicate can be as follows::- module(_, _, [assertions]).
%! \begin{focus}
create_pairs([],[]).
create_pairs([X|R],[(X,X)|S]) :- create_pairs(R,S).
%! \end{focus}In each pair (P,F), P is the smallest power of F that is not in the solution list yet. So, the first component of the first element of the pair-list is the next element in the output we are constructing. We remove this pair, compute the next power of F (i.e., P*F), and insert the pair (P*F,F) into the pair-list, respecting the invariants. We start by writing remove_power/3, which takes a number as first argument, and a list of pairs as second argument, and returns as its third argument another pair-list consisting of the second argument minus the pair (P,F) with P the first argument.:- module(_, _, [assertions]).
%! \begin{focus}
remove_power(_,[],[]).
remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :-
Power =\= Power1, !.
remove_power(Power,[_|RestPFsIn],PFsOut) :-
remove_power(Power,RestPFsIn,PFsOut).
%! \end{focus}We also define sorted_insert/3::- module(_, _, [assertions]).
%! \begin{focus}
sorted_insert([], X, [X]).
sorted_insert([(X1,F1)|L1], (X,F), [(X,F), (X1,F1)|L1]) :- X =< X1, !.
sorted_insert([P|L1], X, [P|L]) :- sorted_insert(L1, X, L).
%! \end{focus}This predicate compares the value of the item to be inserted (the second argument) with the head of the list. If it is less than this value, then the new pair must be inserted just before this head, otherwise the pair is inserted into the new tail.Initial implementation
Using the information we have seen so far we would have the following implementation (there is a brief explanation of each predicate):%! \begin{focus}
:- module(_,[powers/3],[assertions]).
% powers(X,N,P): P is the sorted list that contains the smallest N integers
% that are a non-negative power of one of the elements of the list X.
powers([],_,[]).
powers(Factors,N,Powers) :-
quicksort(Factors, SFactors),
create_pairs(SFactors,Pairs),
first_powers(N,Pairs,Powers).
% quicksort(Xs,Ys): Performs a quicksort of a list Xs and returns the result
% in Ys.
quicksort(Xs,Ys) :- qsort(Xs,Ys,[]).
qsort([],DL,DL).
qsort([X|Xs],Head,Tail) :-
partition(Xs,X,L,R),
qsort(L,Head,[X|QR]),
qsort(R,QR,Tail).
partition([],_,[],[]).
partition([X|Xs],Pv,[X|L],R) :- X =< Pv, !, partition(Xs,Pv,L,R).
partition([X|Xs],Pv,L,[X|R]) :- X > Pv, partition(Xs,Pv,L,R).
% create_pairs(F,P): F is a list and P is sorted list of pairs. Each
% element of P has the form (X,X), where X is a element of F.
create_pairs([],[]).
create_pairs([X|R],[(X,X)|S]) :- create_pairs(R,S).
% first_powers(N,L,R): R is a sorted list with N non-negative numbers.
first_powers(N,[(Power,Factor)|PFs],[Power|Powers]) :-
N > 0, !,
N1 is N-1,
remove_power(Power,PFs,PFs1),
Power1 is Power*Factor,
sorted_insert(PFs1,(Power1,Factor),PFs2),
first_powers(N1,PFs2,Powers).
first_powers(0,_,[]).
% remove_powers(P,L,R): R is the sorted list of pairs obtained by removing
% from the list L.
remove_power(_,[],[]).
remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :-
Power =\= Power1, !.
remove_power(Power,[_|RestPFsIn],PFsOut) :-
remove_power(Power,RestPFsIn,PFsOut).
% sorted_insert(L,P,R): R is the sorted list of pairs obtained by adding
% to the list L the pair P.
sorted_insert([], X, [X]).
sorted_insert([(X1,F1)|L1], (X,F), [(X,F), (X1,F1)|L1]) :- X =< X1, !.
sorted_insert([P|L1], X, [P|L]) :- sorted_insert(L1, X, L).
%! \end{focus}Below are some examples of queries to the powers/3 predicate (make sure that the code box above is marked with a green check mark):?- powers([3,5,4],17,Powers).
?- powers([2,9999999,9999998],20,Powers).
?- powers([2,4],4,Powers).
?- powers([4,2],6,Powers).Hint: Remember that Powers contains the smallest 6 integers (in ascending order) that are a non-negative power of one of the elements of [4,2].
Analysis of our initial implementation
Let us analyze this implementation of the powers/3 predicate. The Ciao system includes a large number of domains that can be used in this program and has strategies for selecting among them. In programs without assertions, such as this one, CiaoPP analyzes the program typically using by default a types domain (the regular types domain eterms) and a modes domain (the sharing/freeness domain shfr). We will be working mainly with these two doamis. The following are the results (it is not necessary to look too carefully into these results yet):
WARNING (ctchecks_pp_messages): (lns 22-22) At literal 1 could not verify assertion: :- check calls B=<A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:=<(A,B) : [eterms] basic_props:term(B),basic_props:term(A),basic_props:term(A),basic_props:term(B),basic_props:term(C) [shfr] native_props:mshare([[B],[B,A],[B,A,B],[B,B],[A],[A],[A,B],[B],[C]]),term_typing:var(A),term_typing:var(C) WARNING (ctchecks_pp_messages): (lns 22-23) At literal 1 could not verify assertion: :- check calls B>A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:>(A,B) : [eterms] basic_props:term(B),basic_props:term(A),basic_props:term(A),basic_props:term(B),basic_props:term(C) [shfr] native_props:mshare([[B],[B,A],[B,A,B],[B,B],[A],[A],[A,B],[B],[C]]),term_typing:var(A),term_typing:var(C) WARNING (ctchecks_pp_messages): (lns 27-39) At literal 1 could not verify assertion: :- check calls A>B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:>(A,B) : [eterms] basic_props:term(A),rt188(B) with: :- regtype rt188/1. rt188(0). [shfr] native_props:mshare([[A]]),term_typing:ground([B]) WARNING (ctchecks_pp_messages): (lns 27-39) At literal 4 could not verify assertion: :- check calls A is B : ( ( var(A), nonvar(B), var(A), arithexpression(B) ); ( var(A), nonvar(B), var(A), intexpression(B) ); ( nonvar(A), nonvar(B), num(A), arithexpression(B) ); ( nonvar(A), nonvar(B), int(A), intexpression(B) ) ). because on call arithmetic:is(A,B) : [eterms] basic_props:term(A),rt201(B) with: :- regtype rt201/1. rt201(A*B) :- term(A), term(B). [shfr] native_props:mshare([[A],[B]]),term_typing:var(A) WARNING (ctchecks_pp_messages): (lns 47-48) At literal 1 could not verify assertion: :- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:=\=(A,B) : [eterms] basic_props:term(A),rt112(A),basic_props:term(B),basic_props:term(B) [shfr] native_props:mshare([[A],[A,A],[A,A,B],[A,A,B,B],[A,A,B],[A,B],[A,B,B],[A,B],[A],[A,B],[A,B,B],[A,B],[B],[B,B],[B]]) WARNING (ctchecks_pp_messages): (lns 56-56) At literal 1 could not verify assertion: :- check calls B=<A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:=<(A,B) : [eterms] rt112(A),basic_props:term(B),basic_props:term(B),basic_props:num(A),arithmetic:arithexpression(C) [shfr] native_props:mshare([[A],[A,B],[A,B,B],[A,B],[B],[B,B],[B]]),term_typing:ground([A,C])
These warnings are stating that there are a number of assertions that cannot be shown to hold. In particular, the analysis is saying that it is not possible to ensure that the calls that the program makes to predicates such as >=/2, </2, >/2, is/2, and =</2 respect the corresponding preconditions or calling modes, which generally require the arguments to be bound to arithmetic expressions when called. The interesting thing to note here is that we did not have to include any assertions in our code. The warning messages stem from the assertions (specifications) that provide the pre-conditions and post-conditions for such library predicates in the Ciao system libraries. Thus, a first observation is that it is possible to identify potential bugs even without actually adding assertions to programs. However, in general, if the program is incorrect, the more assertions are present in the program, the more likely it is for errors to be detected automatically. Thus, we may choose to dedicate more time to writing assertions for those parts of the program that are more likely to be buggy or whose correctness is paticularly important.
In particular, in view of the warnings above, it seems useful to be able to ensure that all these library predicates will always be called properly within our module and thus be more confident about our program. We can work towards this objective by providing some information regarding how the exported predicate, powers/3, will be called from outside the module.
Using assertions
For example, from the problem specification we know that the second argument should always be a number. In order to be able to state such properties of predicates we will have to use the assertion language. A particularly useful type of assertions for describing predicates are pred assertions. Such assertions use the following syntax:
:- pred Pred [:Precond] [=> Postcond] [+ CompProp] .Such an assertion indicates that in any call to Pred, if Precond holds in the calling state and the computation of the call succeeds, then Postcond also holds in the success state. As we will see later, Precond and Postcond are conjunctions of state properties. CompProp refers to the sequence of states during excution of the predicate and we refer to the properties that appear there as properties of the computation. Examples are determinacy, non-failure, or cost.
So, we can start by adding the following pred assertion to state that when powers/3 is called the second argument is bound to a number, using the built-in property num/1:
:- pred powers(A,B,C) : num(B).We then proceed to run CiaoPP again:
WARNING (ctchecks_pp_messages): (lns 23-23) At literal 1 could not verify assertion: :- check calls B=<A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:=<(A,B) : [eterms] basic_props:term(B),basic_props:term(A),basic_props:term(A),basic_props:term(B),basic_props:term(C) [shfr] native_props:mshare([[B],[B,A],[B,A,B],[B,B],[A],[A],[A,B],[B],[C]]),term_typing:var(A),term_typing:var(C) WARNING (ctchecks_pp_messages): (lns 24-24) At literal 1 could not verify assertion: :- check calls B>A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:>(A,B) : [eterms] basic_props:term(B),basic_props:term(A),basic_props:term(A),basic_props:term(B),basic_props:term(C) [shfr] native_props:mshare([[B],[B,A],[B,A,B],[B,B],[A],[A],[A,B],[B],[C]]),term_typing:var(A),term_typing:var(C) WARNING (ctchecks_pp_messages): (lns 28-35) At literal 4 could not verify assertion: :- check calls A is B : ( ( var(A), nonvar(B), var(A), arithexpression(B) ); ( var(A), nonvar(B), var(A), intexpression(B) ); ( nonvar(A), nonvar(B), num(A), arithexpression(B) ); ( nonvar(A), nonvar(B), int(A), intexpression(B) ) ). because on call arithmetic:is(A,B) : [eterms] basic_props:term(A),rt201(B) with: :- regtype rt201/1. rt201(A*B) :- term(A), term(B). [shfr] native_props:mshare([[A],[B]]),term_typing:var(A) WARNING (ctchecks_pp_messages): (lns 39-40) At literal 1 could not verify assertion: :- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:=\=(A,B) : [eterms] basic_props:term(A),rt112(A),basic_props:term(B),basic_props:term(B) [shfr] native_props:mshare([[A],[A,A],[A,A,B],[A,A,B,B],[A,A,B],[A,B],[A,B,B],[A,B],[A],[A,B],[A,B,B],[A,B],[B],[B,B],[B]]) WARNING (ctchecks_pp_messages): (lns 45-45) At literal 1 could not verify assertion: :- check calls B=<A : ( nonvar(B), nonvar(A), arithexpression(B), arithexpression(A) ). because on call arithmetic:=<(A,B) : [eterms] rt112(A),basic_props:term(B),basic_props:term(B),basic_props:num(A),arithmetic:arithexpression(C) [shfr] native_props:mshare([[A],[A,B],[A,B,B],[A,B],[B],[B,B],[B]]),term_typing:ground([A,C])
As we can see, CiaoPP continues producing some warning messages but they are now fewer.
Regular types and other properties
We have seen before that certain properties are used in the assertions that describe predicates. Some of these properties, like num/1, var/1, or not_fails, are builtins, defined in libraries. However, we can also define new properties, including new regular types, which are a particular kind of property. In general, properties (and therefore types) are normal predicates, but which meet certain conditions (e.g., termination) and are marked as such via prop/1 or regtype/1 declarations. See the section of Declaring regular types in the CiaoPP manual for more details on (regular) types, as well as other details about properties in Ciao. For example, our specification states that the first argument is a list of numbers. This property is available in the Ciao libraries, however, we choose here to declare it ourselves. So we represent the set of "lists of numbers" by the regular type list_num, defined as follows:
:- regtype list_num(X) # "@var{X} is a list of numbers." .
list_num([]).
list_num([X|T]) :-
num(X), list_num(T). The problem specification also tells us that the first argument is a list of numbers and that powers/3 returns another number list of numbers (for now, we will not put other restrictions such as being a list of non-negative numbers). I.e., combining with the previous information, we need to ensure that for any call to predicate powers/3 with the first argument bound to a list of numbers, the second argument bound to a number, and the third one unbound, if the call succeeds, then the third argument will also be bound to a list of numbers.
%! \begin{code}
:- pred powers(A,B,C) : (?, ?, ?) => (?) .
%! \end{code}
%! \begin{opts}
solution=equal
%! \end{opts}
%! \begin{solution}
:- pred powers(A,B,C) : (list_num(A), num(B), var(C)) => (list_num(C)).
%! \end{solution}If we now run CiaoPP we will see that there are no warning messages produced (and also none in the file generated by CiaoPP), i.e., CiaoPP can now prove that all calls to library predicates are correct and will not raise any errors at run time (we will return to this topic later). Furthermore, we will find in the output the following assertion:
%% %% :- check pred powers(A,B,C) %% %% : ( list_num(A), num(B), var(C) ) %% %% => list_num(C). :- checked calls powers(A,B,C) : ( list_num(A), num(B), var(C) ). :- checked success powers(A,B,C) : ( list_num(A), num(B), var(C) ) => list_num(C).
This means that the assertion that we have included has been marked as checked, i.e., it has been validated, proving that indeed the third argument of powers/3 will be bound to a list of numbers on success.
If we take a look again into the file generated by CiaoPP we will find these assertions:
:- true pred remove_power(_1,_A,PFsOut) : ( num(_1), list(^(('basic_props:num','basic_props:num')),_A), term(PFsOut) ) => ( num(_1), list(^(('basic_props:num','basic_props:num')),_A), list(^(('basic_props:num','basic_props:num')),PFsOut) ).
:- true pred remove_power(_1,_A,PFsOut) : ( mshare([[PFsOut]]), var(PFsOut), ground([_1,_A]) ) => ground([_1,_A,PFsOut]).
The sharing and freeness analysis abstract domain computes freeness, independence, and grounding dependencies between program variables. The second assertion expresses that, when remove_power/3 is called (:) the third argument is a free variable, while the first and second arguments are input values (i.e., ground on call). This second assertion also states that on success all three arguments will get instantiated. On the other hand, the first assertion expresses that, if remove_power(N, A, B) is called with a number N, a pair-list of numbers in A, and any term in B, then B will on exit be a pair-list of numbers. Therefore, we need a regular type list_pair which defines a list of pairs (X,Y). If we continue to examine the output of CiaoPP we can see this other assertion:
:- true pred sorted_insert(_A,X,_B) : ( list(^(('basic_props:num','basic_props:num')),_A), rt96(X), term(_B) ) => ( list(^(('basic_props:num','basic_props:num')),_A), rt96(X), list1(^((num,num)),_B) ).
:- regtype rt51/1. rt51([]). rt51([A|B]) :- num(A), term(B). :- regtype rt96/1. rt96((A,B)) :- num(A), num(B).
where we find new types, inferred by CiaoPP. The analyzer thus tells us about types that represent the data that the program builds, and we can use these definitions back in the source file to enhance the specification. In our case, the second regular type is defining the pairs, so we can copy it into the source file, giving it a meaningful name for clarity, as follows:
:- regtype num_pair(P) .
num_pair((X, Y)):-
num(X),
num(Y).
:- regtype list_pair(L) .
list_pair([]).
list_pair([X|Xs]):-
num_pair(X),
list_pair(Xs).
:- regtype list_pair1(L) .
list_pair1([X|Xs]):-
num_pair(X),
list_pair(Xs). (Note that we can also use parametric types here, but we use a simple type for simplicity.) Once we have defined these regular types, we can write more precise assertions:
%! \begin{code}
:- pred remove_power(A,B,C) : (?, ?, ?) => (?) .
%! \end{code}
%! \begin{opts}
solution=equal
%! \end{opts}
%! \begin{solution}
:- pred remove_power(A,B,C) : (num(A), list_pair(B), var(C)) => list_pair(C).
%! \end{solution}%! \begin{code}
:- pred sorted_insert(A,B,C) : (?, ?, ?) => (?) .
%! \end{code}
%! \begin{opts}
solution=equal
%! \end{opts}
%! \begin{solution}
:- pred sorted_insert(A,B,C) : (list_pair(A), num_pair(B), var(C)) => list_pair1(C).
%! \end{solution}Using the information we have seen so far we would have the following implementation:
%! \begin{focus}
:- module(_,[powers/3],[assertions, regtypes, nativeprops]).
:- regtype list_num(X) .
list_num([]).
list_num([X|T]) :-
num(X),
list_num(T).
%! powers(X,N,P): `P` is the sorted list that contains the smallest `N` integers
% that are a non-negative power of one of the elements of the list `X`.
:- pred powers(A,B,C) : (list_num(A), num(B), var(C)) => (list_num(C)).
powers([],_,[]).
powers(Factors,N,Powers) :-
quicksort(Factors, SFactors),
create_pairs(SFactors,Pairs),
first_powers(N,Pairs,Powers).
%! quicksort(Xs,Ys): Performs a quicksort of a list `Xs` and returns the
% result in `Ys`.
quicksort(Xs,Ys) :- qsort(Xs,Ys,[]).
qsort([],DL,DL).
qsort([X|Xs],Head,Tail) :-
partition(Xs,X,L,R),
qsort(L,Head,[X|QR]),
qsort(R,QR,Tail).
partition([],_,[],[]).
partition([X|Xs],Pv,[X|L],R) :- X =< Pv, !, partition(Xs,Pv,L,R).
partition([X|Xs],Pv,L,[X|R]) :- X > Pv, partition(Xs,Pv,L,R).
%! create_pairs(F,P): `F` is a list and `P` is sorted list of pairs.
% Each element of `P` has the form `(X,X)`, where `X` is a element of `F`.
create_pairs([],[]).
create_pairs([X|R],[(X,X)|S]) :- create_pairs(R,S).
:- regtype num_pair(P) .
num_pair((X, Y)):- num(X), num(Y).
:- regtype list_pair(L).
list_pair([]).
list_pair([X|Xs]):-
num_pair(X),
list_pair(Xs).
:- regtype list_pair1(L).
list_pair1([X|Xs]):-
num_pair(X),
list_pair(Xs).
%! first_powers(N,L,R): `R` is a sorted list with `N` non-negative numbers.
% includedef{first_powers/3}
:- pred first_powers(A,B,C) : (num(A), list_pair(B),var(C)) => (list_num(C)) .
first_powers(N,[(Power,Factor)|PFs],[Power|Powers]) :-
N > 0, !,
N1 is N-1,
remove_power(Power,PFs,PFs1),
Power1 is Power*Factor,
sorted_insert(PFs1,(Power1,Factor),PFs2),
first_powers(N1,PFs2,Powers).
first_powers(0,_,[]).
%! remove_powers(P,L,R): `R` is the sorted list of pairs obtained by removing from the list `L`
% the pair (`P`,_).
:- pred remove_power(A,B,C) : (num(A), list_pair(B), var(C)) => list_pair(C) .
remove_power(_, [], []).
remove_power(Power, [(Power1, Factor)|RestOut], [(Power1, Factor)|RestOut]) :-
Power == Power1, !.
remove_power(Power, [_|RestPFsIn], PFsOut) :-
remove_power(Power, RestPFsIn, PFsOut).
%! sorted_insert(L,P,R): `R` is the sorted list of pairs obtained by adding to the list `L`
% the pair `P`.
:- pred sorted_insert(A,B,C) : (list_pair(A), num_pair(B), var(C)) => list_pair1(C) .
sorted_insert([], X, [X]).
sorted_insert([(X1,F1)|L1], (X,F), [(X,F), (X1,F1)|L1]):- X =< X1, !.
sorted_insert([X1|L1], X, [X1|L]):- sorted_insert(L1, X, L).
%! \end{focus}If we now run CiaoPP on this file all the assertions that we have written are proved to hold (no errors are reported).Bugs detected by CiaoPP
In the sections above we have included assertions to describe some properties that we require to hold of our program. But we also mentioned that CiaoPP can identify errors without these assertions. So imagine we make some modifications to the predicate remove_power/3 defined above::- module(_,[remove_power/3],[assertions]).
remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :-
Power =\= power1, !.
remove_power(Power,[_|RestPFsIn],PFsOut) :-
remove_power(Power,RestPFsIn,PFsOut1). If we now run CiaoPP it produces the following output:
WARNING: (lns 5-6) [PFsOut,PFsOut1] - singleton variables in remove_power/3 WARNING (preproc_errors): (lns 2-4) goal arithmetic:=\=(Power,power1) at literal 1 does not succeed! WARNING (preproc_errors): (lns 5-6) goal remove_power_bug1:remove_power(Power,RestPFsIn,PFsOut1) at literal 1 does not succeed! ERROR (ctchecks_pp_messages): (lns 2-4) At literal 1 false assertion: :- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:=\=(A,B) : [eterms] basic_props:term(A),rt2(B) with: :- regtype rt2/1. rt2(power1).
As we can see, different messages appear. In this section, we will explain one by one what each of these messages indicates, and how we can take care of them:
- Singleton variable: The first message is a warning message which indicates that there are singleton variables. Singleton variables are those which appear only one time in a clause. As mistyping a variable is a common mistake, CiaoPP outputs a warning message if a variable is used only once (such warnings would also be emitted by the compiler).Exercise 5 (Detecting Bugs). What variable do you need to change? (Only change the incorrect variable.)
:- module(_,[remove_power/3],[assertions]). %! \begin{code} remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut1). %! \end{code} %! \begin{opts} solution=errors,message=singleton %! \end{opts} %! \begin{solution} remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut). % In our case, we type PFsOut1 instead of PFsOut. %! \end{solution} - No base case: The fact that a predicate always fails is not sufficient to conclude that there is a bug in the program. However, in most cases this is actually a bug, as is the case in this program. Predicate remove_power/3 is called recursively but has no base case, this means it will either loop or fail. So, we add the following base case and fix the error:
:- module(_,[remove_power/3],[assertions]). remove_power([],[]). remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut).We now obtain the following messages:
WARNING: (lns 4-5) predicate remove_power/3 is already defined with arity 2 WARNING (preproc_errors): (lns 4-5) goal arithmetic:=\=(Power,power1) at literal 1 does not succeed! WARNING (preproc_errors): (lns 6-7) goal remove_power_bug3:remove_power(Power,RestPFsIn,PFsOut) at literal 1 does not succeed! ERROR (ctchecks_pp_messages): (lns 4-5) At literal 1 false assertion: :- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:=\=(A,B) : [eterms] basic_props:term(A),rt2(B) with: :- regtype rt2/1. rt2(power1).
- Arity: We have forgotten a parameter in the base case of the recursive predicate remove_power/3. Then, CiaoPP detects that two predicates: remove_power/2 and remove_power/3 are defined, so it is possible that we have forgotten or added an argument in one of them (these warnings are also detected by the compiler and can also be turned off when using multi-arity declarations).Exercise 6 (Detecting Bugs). What is the correct base case?
%! \begin{code} :- module(_,[remove_power/3],[assertions]). remove_power([],[]). remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut). %! \end{code} %! \begin{opts} solution=errors,message=arity %! \end{opts} %! \begin{solution} :- module(_,[remove_power/3],[assertions]). remove_power(_,[],[]). remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut). %! \end{solution} - Static Checking of Assertions in System Libraries: As mentioned before, CiaoPP can find incompatibilities in the ways in which library predicates are called. In our example =\=/2 is a library predicate so suppose that inadvertently a bug was introduced in the second clause of remove_power/3, and instead of writing Power1 we wrote power1 (it is a bug since variables always begin with a capital letter). We run CiaoPP again:
ERROR (ctchecks_pp_messages): (lns 4-5) At literal 1 false assertion: :- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ). because on call arithmetic:=\=(A,B) : [eterms] basic_props:term(A),rt9(B) with: :- regtype rt9/1. rt9(power1).Note that CiaoPP tells us that the arithmetic library in Ciao contains an assertion of the form:
:- check calls A=\=B : ( nonvar(A), nonvar(B), arithexpression(A), arithexpression(B) ).
which requires the second argument of =\=/2 to be an arithmetic expression (which is a regular type also defined in the arithmetic library) that contains no variables. Moreover, the eterms analysis indicates to us that in our program A is any term and B is an auxiliary regular type which was created by CiaoPP to represent the constant power1.Exercise 7 (Detecting Bugs). Although we have seen the predicate without bugs, try to write it again without any errors.:- module(_,[remove_power/3],[assertions, regtypes, nativeprops]). :- regtype list_num(X). list_num([]). list_num([X|T]) :- num(X), list_num(T). :- regtype list_num1(X). list_num1([X|T]) :- num(X), list_num(T). :- regtype num_pair(P). num_pair((X, Y)) :- num(X), num(Y). :- regtype list_pair(L). list_pair([]). list_pair([X|Xs]) :- num_pair(X), list_pair(Xs). :- regtype list_pair1(L). list_pair1([X|Xs]) :- num_pair(X), list_pair(Xs). %! \begin{code} :- pred remove_power(A,B,C) : (num(A), list_pair(B), var(C)) => list_pair(C). remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :- Power =\= power1, !. remove_power(Power,[_|RestPFsIn],PFsOut) :- remove_power(Power,RestPFsIn,PFsOut1). %! \end{code} %! \begin{opts} A,solution=errors %! \end{opts} %! \begin{solution} :- pred remove_power(A,B,C) : (num(A), list_pair(B), var(C)) => list_pair(C). remove_power(_, [], []). remove_power(Power, [(Power1, Factor)|RestOut], [(Power1, Factor)|RestOut]) :- Power =\= Power1, !. remove_power(Power, [_|RestPFsIn], PFsOut) :- remove_power(Power, RestPFsIn, PFsOut). %! \end{solution}
We can see that no error (false assertion) is now detected in the calls to the arithmetic library, although we still have some assertions that are not proved.
Nonfailure+Determinism Domain
So far we have only worked with the two most used abstract domains: shfr and eterms. However, CiaoPP has a wide variety of abstract domains to perform analysis with. In this section, we will analyze the example with nfdet analysis. The nfdet combined domain carries nonfailure (nf) and determinism (det) information, i.e., the analysis will be able to detect procedures that can be guaranteed not to fail (produce at least one solution) and to detect predicates which are deterministic (produce at most one solution).
Categories
The following lattice diagram summarizes several determinacy and nonfailure properties inferred by the nf and det domains:
nondet [0,inf]
/ \
/ \
semidet [0,1] multi [1,inf]
/ \ /
/ \ /
fails [0,0] det [1,1]
\ /
\ /
bottom (non reachable) - semidet = 0 or 1 solutions
- multi = 1 or more solutions
- det = 1 solution
- fails = 0 solutions
Example: sorted_insert/3
In order to see these analyses in action, assume that our predicate sorted_insert/3 is defined without the cut. If we analyze the program with this modification:
:- module(_, [sorted_insert/3], [assertions,regtypes]).
:- regtype num_pair(P).
num_pair((X, Y)) :- num(X), num(Y).
:- regtype list_pair(L).
list_pair([]).
list_pair([X|Xs]) :-
num_pair(X),
list_pair(Xs).
:- regtype list_pair1(L).
list_pair1([X|Xs]) :-
num_pair(X),
list_pair(Xs).
%! \begin{code}
:- pred sorted_insert(A,B,C) : (list_pair(A), num_pair(B), var(C)) => list_pair1(C).
sorted_insert([], X, [X]).
sorted_insert([(X1,F1)|L1], (X,F), [(X,F), (X1,F1)|L1]) :- X =< X1.
sorted_insert([P|L1], X, [P|L]) :- sorted_insert(L1, X, L).
%! \end{code}
%! \begin{opts}
A,ana_det=nfdet,name=sorted_insert,filter=tpred_plus
%! \end{opts}the output includes the following assertions:
%% %% :- check pred sorted_insert(A,B,C) %% %% : ( list_pair(A), num_pair(B), var(C) ) %% %% => list_pair1(C). :- checked calls sorted_insert(A,B,C) : ( list_pair(A), num_pair(B), var(C) ). :- checked success sorted_insert(A,B,C) : ( list_pair(A), num_pair(B), var(C) ) => list_pair1(C).
Thus, we can see that the analyzer does verify the assertion that we had included. However, we can also see these other assertions:
:- true pred sorted_insert(A,B,C) : ( mshare([[C]]), var(C), ground([A,B]), list_pair(A), num_pair(B), term(C) ) => ( ground([A,B,C]), list_pair(A), num_pair(B), list_pair1(C) ) + ( multi, covered, possibly_not_mut_exclusive ). :- true pred sorted_insert(A,B,C) : ( mshare([[C]]), var(C), ground([A,B]), list_pair(A), num_pair(B), term(C) ) => ( ground([A,B,C]), list_pair(A), num_pair(B), list_pair1(C) ) + ( multi, covered, possibly_not_mut_exclusive ).
As we mentioned before, the + field in pred assertions describes properties of the computation of the predicate (such as determinism or non-failure). According to the diagram shown before, multi states that there is at least one solution but may have more. Also, covered means that for any input there is at least one clause whose succeeds and possibly_not_mut_exclusive denotes that mutual exclusion is not ensured. This is because when the first argument is a non-empty list both the second and third clauses will succeed. When reasoning about determinacy, it is a necessary condition (but not sufficient) that clauses of the predicate be pairwise mutually exclusive, i.e., that only one clause will produce solutions. In order to solve this, we can add either the complementary X > X1 condition in the third clause or the cut in the second clause. Obviously, for any particular call only one of the clauses X =< X1 or X > X1 will succeed. Adding one of these two options and analyzing the program again we can see that the predicate is deterministic (modifying the previous example you can observe this behavior).
Dynamic Bug Finding with CiaoPP's Testing Facilities
The specification throughout our program so far is that the predicate powers/3 is called with a list of numbers as first argument, a number N as second argument, and a free variable in the third argument. However, the original specification states that the numbers are actually non-negative integers. It also states that the list produced on success in the third argument is also a list of non-negative integers, and, furthermore, that this list is in ascending order (i.e., sorted in ascending order).
We can specify all this by first defining new properties as follows (we use nnegint from the Ciao libraries):
:- prop sorted/1.
sorted([]).
sorted([_]).
sorted([X,Y|Ys]) :-
X=<Y,
sorted([Y|Ys]).
:- prop list_nnegint(X) + regtype
# "Verifies that @var{X} is list of non-negative integers." .
list_nnegint([]).
list_nnegint([X|T]) :-
nnegint(X),
list_nnegint(T). list_nnegint/1 checks if the argument is a list of non-negative integers, sorted/1 checks if the argument is a sorted list. Other properties like var/1 or not_fails are builtins, defined in libraries. These properties are important because they will be used by CiaoTest as generators for test cases. Then including them in our program together with the following assertion:
:- pred powers(A,B,C) : (list_nnegint(A), nnegint(B), var(C)) => (list_nnegint(C), sorted(C)) + not_fails.and running CiaoPP we will see that this assertion cannot be proved nor disproved statically with the standard CiaoPP domains:
:- check success powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ) => ( list_nnegint(C), sorted(C) ). :- check comp powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ) + not_fails. :- checked calls powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ).
This is because there is no abstract domain that covers properly the sorted/1 property. This is something that can occur specially with user-defined properties. In these cases CiaoPP will generate run-time checks for the properties that have not been verified statically in such assertions. Such runtime checks will raise an error if the assertion is violated, albeit at run time. Thus, they at least ensure that execution paths that violate the assertions are captured during execution.
Since letting errors be raised after deployment is less desirable, a step that can be taken in order to deal with non-verified assertions is to generate test cases to try to find a counterexample, i.e., an input for which an error is raised by the run-time tests. This can be done either manually, by adding test assertions (unit tests), to the program, or using the provisions that CiaoPP offers for automatically generating test cases from the call fields of assertions. This process works as follows:
Consider this buggy implementation of quicksort/2 in powers/3:
:- module(_,[powers/3],[assertions,nativeprops]).
:- prop list_nnegint(X) + regtype .
list_nnegint([]).
list_nnegint([X|T]) :-
nnegint(X), list_nnegint(T).
:- prop sorted(Xs).
sorted([]).
sorted([_]).
sorted([X,Y|Ns]) :-
X =< Y,
sorted([Y|Ns]).
%! \begin{focus}
:- pred powers(A,B,C) : (list_nnegint(A), nnegint(B), var(C)) => (list_nnegint(C), sorted(C) ) + not_fails.
:- test powers(A,B,C) : (A = [3,4,5], B = 17) => (C = [3,4,5,9,16,25,27,64,81,125,243,256,625,729,1024,2187,3125]) + not_fails.
:- test powers(A,B,C) : (A = [2,9999999,9999998], B = 20) => (C = [2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072,262144,524288,1048576]) + not_fails.
:- test powers(A,B,C) : (A = [2,4], B = 6) => (C = [2,4,8,16,32,64]) + not_fails.
powers([],_,[]).
powers(Factors,N,Powers) :-
quicksort(Factors, SFactors),
create_pairs(SFactors,Pairs),
first_powers(N,Pairs,Powers).
% qsort with a slight mistake: it may fail when there are repeated numbers in the list
quicksort(Xs,Ys) :- qsort(Xs,Ys,[]).
qsort([],DL,DL).
qsort([X|Xs],Head,Tail) :-
partition(Xs,X,L,R),
qsort(L,Head,[X|QR]),
qsort(R,QR,Tail).
partition([],_,[],[]).
partition([X|Xs],Pv,[X|L],R) :- X < Pv, !, partition(Xs,Pv,L,R). % (1) should be >= (or =< below)
partition([X|Xs],Pv,L,[X|R]) :- X > Pv, partition(Xs,Pv,L,R).
%! \end{focus}
create_pairs([],[]).
create_pairs([X|R],[(X,X)|S]) :- create_pairs(R,S).
first_powers(N,[(Power,Factor)|PFs],[Power|Powers]) :-
N > 0, !,
N1 is N-1,
remove_power(Power,PFs,PFs1),
Power1 is Power*Factor,
sorted_insert(PFs1,(Power1,Factor),PFs2),
first_powers(N1,PFs2,Powers).
first_powers(0,_,[]).
remove_power(_,[],[]).
remove_power(Power,[(Power1,Factor)|RestOut],[(Power1,Factor)|RestOut]) :-
Power =\= Power1, !.
remove_power(Power,[_|RestPFsIn],PFsOut) :-
remove_power(Power,RestPFsIn,PFsOut).
sorted_insert([], X, [X]).
sorted_insert([(X1,F1)|L1], (X,F), [(X,F), (X1,F1)|L1]) :- X =< X1, !.
sorted_insert([P|L1], X, [P|L]) :- sorted_insert(L1, X, L).This predicate sorts a given list of integers from lowest to highest. However, we have introduced an intentional bug (1 in the listing) that causes the program to fail when a list with repeated elements is given.After the pred assertion we can see three test assertions that the user has included to check the behavior of the predicate. They cover the examples given in the problem statement.
Setting up CiaoPP flags
In order to carry out the operations described above (running unit tests and test generation) automatically we need to activate a few flags in CiaoPP's menu. Under the Test assertions category, we will find the Run test assertions (run_utests) and Generate tests from check assertions (test_gen) flags that we need to turn on:
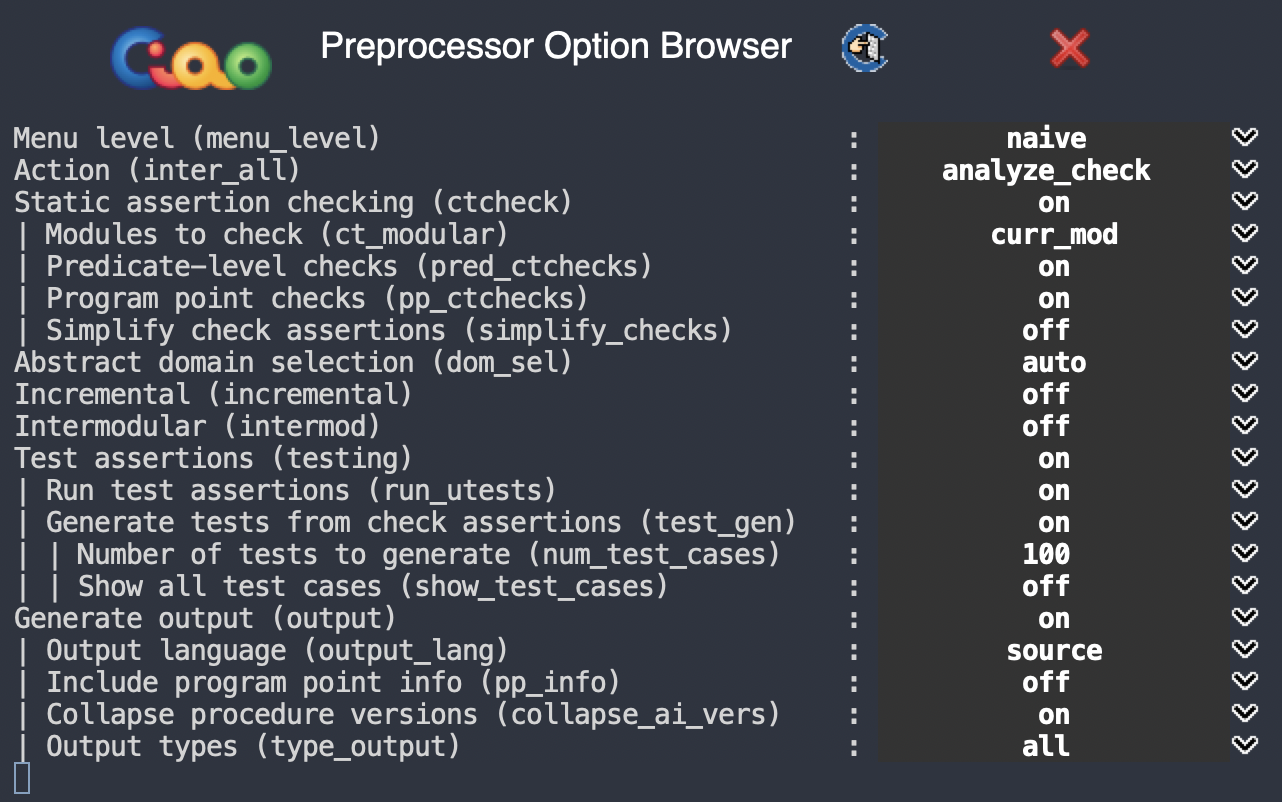
Now, when we tell CiaoPP to perform assertion checking, it will first run the usual static analysis and checking of assertions, then it will run all unit tests present in the program. If at least one of them fails, then random test generation is skipped. However, if all unit tests pass, test generation is performed as a last step to try to find test cases that make the assertions fail, hence revealing faults in our code.
Running unit tests
After assertion checking, CiaoTest runs all unit tests present in the program:
:- checked test powers(A,B,C) : ( (A=[3,4,5]), (B=17) ) => (C=[3,4,5,9,16,25,27,64,81,125,243,256,625,729,1024,2187,3125]) + not_fails. :- checked test powers(A,B,C) : ( (A=[2,9999999,9999998]), (B=20) ) => (C=[2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072,262144,524288,1048576]) + not_fails. :- checked test powers(A,B,C) : ( (A=[2,4]), (B=6) ) => (C=[2,4,8,16,32,64]) + not_fails.
In this case all tests passed without errors, so random test generation is performed.
Generating Tests
CiaoTest will read the assertions left to be checked and generate goals for that predicate satisfying the assertion precondition and execute them to either check that the assertion holds for those cases or find errors. Lets see what CiaoTest did:
ERROR: (lns 19-20) Failed test for predicate: power_testing_eterms_nf_shfr_co:powers(A,B,C). Test case: powers([72,72,92,95,58],13,_). In *comp*, unsatisfied property: not_fails. Where: fails ERROR: (lns 81-82) Failed in power_testing_eterms_nf_shfr_co:powers(A,B,C).
By default CiaoTest generates 100 cases for each assertion, or stops before if it finds one case that does not meet the assertion post-condition. Keep in mind that the generation is random, so do not expect to get the same results if you try this yourself, in fact, it may very well be that none of the test cases generated makes the program fail, so it is recommended to run CiaoTest a couple times or increase the number of cases to be generated using the num_test_cases option in CiaoPP's flags menu. For that same reason, it is also important to note that of course even if CiaoTest does not find any cases that violate the assertion, one cannot affirm that the assertion is true.
The failed test cases that we got are valid calls to powers/3 that did not comply with the post-condition, in particular, they violated the computational properties field, since they where required to not fail. Thus, they are counter-examples that prove that the remaining part of the assertion does not hold. Now we are aware that the predicate is not behaving as it should. If we look at the input lists that violate the assertion, it is not too difficult too realize that there are repeated elements in them, and that this may be the source of our problems.
If it is not apparent where the bug is through observation, a good next step would be to debug the predicate in the interactive source debugger calling it with the counter-examples that CiaoTest generated for us and look for the point in which the error occurs.
If we take a look into CiaoPP's output file now, we will see that some of the assertions left to be checked after static analysis have been proven false by the counter-examples found via test generation:
:- check success powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ) => ( list_nnegint(C), sorted(C) ). :- checked calls powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ). :- false comp powers(A,B,C) : ( list_nnegint(A), nnegint(B), var(C) ) + ( not_fails, by((texec 4)) ). :- checked test powers(A,B,C) : ( (A=[3,4,5]), (B=17) ) => (C=[3,4,5,9,16,25,27,64,81,125,243,256,625,729,1024,2187,3125]) + not_fails. :- checked test powers(A,B,C) : ( (A=[2,9999999,9999998]), (B=20) ) => (C=[2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072,262144,524288,1048576]) + not_fails. :- checked test powers(A,B,C) : ( (A=[2,4]), (B=6) ) => (C=[2,4,8,16,32,64]) + not_fails.In the computation properties field of the assertions that have been marked as false, we can see a new property by/1 that is used to indicate the source of the failure. In our case, that source is the failed test cases, which are represented by texec declarations, each identified by a different id/1, which is what appears in the by/1 field.
In this section we showed how given a buggy program we can follow a simple methodology to help us spot those bugs. CiaoPP's analyzers and verifiers offer us the static analysis tools to check part of the assertions and then we can ask it to use CiaoTest to check the remaining unchecked assertions by running the unit tests present in the program and with assertion-based random test generation. Depending on the properties involved, this procedure can often be fully automatic, just needing setting the relevant flags. If failing test cases are found they can be excellent starting points for more classical debugging. Other possible approaches include implementing a new abstract domain for a specific property (i.e., in this case a new domain that infers if a list is sorted or not) or proving the property by hand or with an automatic theorem prover. These solutions are more powerful than testing, in the sense that they can potentially verify that there are no errors in the program, while testing can find bugs but cannot verify that there are none, but they are also more involved.
